Minimize Ladder Length over Wall

Some time ago somebody had to solve this math optimization question for their studies and told me about it.

So there is a wall with height h, which has the distance a from a very high "building" and your task, should you accept it, is to find the shortest ladder over the wall that touches the ground and the "building".

So the function to minimize is L = sqrt((x+a)^2+(h+y)^2).
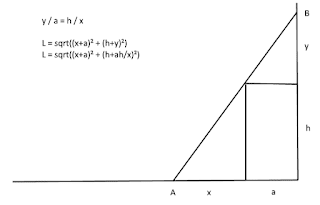
Because we know that y/a = h/x it follows that y = ah/x.
Using this the length become L = sqrt((x+a)^2+(h+ah/x)^2)
The minimum of that function is not changed if we leave out the sqrt and the derivation of (x+a)^2+(h+ah/x)^2 is (2 (a + x) (-a h^2 + x^3))/x^3
So the minimum x is where this function equals zero, which is if x³ = ah²,
and the length then is L = (a^(2/3) + h^(2/3))^3
 
Now the thing that I find strange. Please look at this drawing (which is not really correct because the two "y" do not have the same length).

If the angle ACD is 90° then the ladder has minimal length!
We know that ah=xy, so let's square that: a²h²=x²y² and because ACD is 90° xa=y² which yields

a²h²=x²xa and that gives x³=ah² which is exactly what we got by using the calculus.

Do you have a geometric explanation why L is minimal if ACD is 90°?